一個程式可以說是由資料結構與演算法共同組成......

什麼是資料結構?

資料結構為將資料在記憶體中儲存與管理的方式。它影響資料存取、讀取、修改、刪除的效率。對於不同目的，我們可以透過使用不同的資料結構，來提升效率。
資料結構有分為:

• Primative (基元資料結構): 像是整數(integer), 浮點數(float), 字串(String), 布林 (Boolean)
• Non-Primative (非基元資料結構): 又分成線性(Linear)和非線性(Non-linear)資料結構
  • 線性(in sequential order): List, Tuple, Array, Linked List, Stack, Queue
  • 非線性: Set, Dictionary, Tree, Graph
    其中 List, Tuple, Set, Dictionary為python內建的資料結構，其餘可以通過套件或是自己寫。

什麼是演算法?

演算法指的是一系列清晰的指令來用來執行計算/完成一個任務。包含輸入，計算，得到輸出停止。

教科書裡常見的演算法有以下幾種:
排序 (Sorting):將資料由小到大或大到小排序。
搜尋 (Search):在資料中尋找特定值
圖 (Graph): 用算可以用圖表示的資料
遞迴(Recursive): 解決問題的方式為將問題拆解成數個類似的子問題，反覆呼叫，直到達到 base condition。
貪婪演算法 (Greedy Algorithm): 解決問題的方式為將問題拆解成數個子問題後，找每個階段的local optimal (局部最佳解)，期望找到的局部最佳解為global optimal(全域最佳解)。
分冶法 (Divide and Conquer): 解決問題的方式為將問題拆解成數個子問題後，分別獨立解決每一個子問題，然後再結合統整結果。
動態規劃 (Dynamic Programming): 解決問題的方式為將問題拆解成數個有重疊的子問題，將重複的問題儲存成table或array，可以重複使用，進而減少運算。

既然資料結構與演算法是為了提升程式的效能，那麼如何衡量效能則會是我們在學習資料結構與演算法前必須要先了解的。

衡量程式效能: Big O Notation

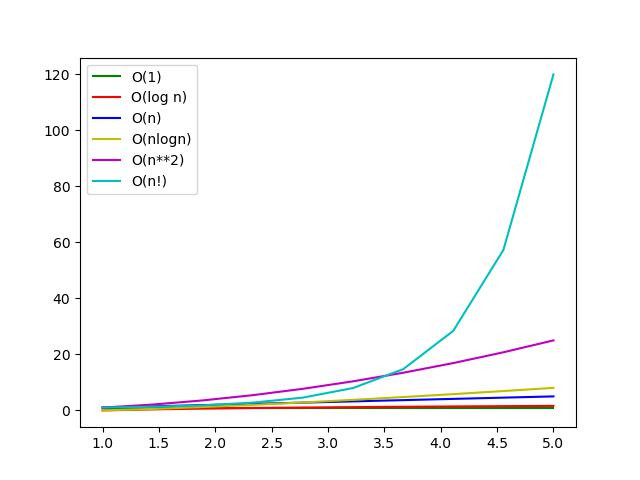
Big O 代表的是最差情況下的程式執行時間與資料量(n)之間的關係 。 在計算時，會把係數、常數直接銷掉，常見的時間複雜度由快到慢為O(1), O(logn), O(n), O(nlogn), O(n^2), O(2^n), O(n!)。(好: O(1), O(logn), O(n)、尚可: O(nlogn)、差: O(n^2), O(2^n), O(n!))以下分別介紹:

O(1): constant time complexity (常數時間，效率最佳)
執行時間不會隨著輸入資料量增加而增加。像是if 判斷式，命某參數特定值，所需時間為O(1)。

def example_constant(n):
    return 10*n+100000
example_constant(10)

def find_element(pos):
    array=[1,2,3,4,5]
    return array[pos]
find_element(1)

O(log n): log time complexity (對數時間，以2為底，效率佳)
執行時間隨資料量增加對數增加(其增加量遠少於線性時間)。當迴圈的每一步，進入的資料逐漸對半減少時，會有此時間複雜度。例如二元搜尋法，每次將資料分成兩份(大於中間值到尾或小於中間值到頭)，搜尋其中一份直到找到目標。(二元搜尋法的例子後面幾天會介紹)

def example_logn(n):
    sum=0
    i=1
    while i<n:
        sum+=i
        i=i*2
        print(i)
example_logn(32)

import math
def BinarySearch(array,target):
    start=0
    end=len(array)-1
    mid=math.floor((start+end)/2)
    while not (array[mid]==target or start>=end):
        if target<array[mid]:
            end=mid-1
        else:
            start=mid+1
        mid=math.floor((start+end)/2)
    if array[mid]==target:
        return mid
    else:
        return 'The value is not found!'
mylist=[1,5,10,25,30,35,40]
print(BinarySearch(mylist,30))

O(n): linear time complexity (線性時間，效率佳)
執行時間會隨著資料量線性增加。通常一層簡單的for迴圈即可以有此效果。

def example_linear(n):
    for i in range(n):
        print(i*2)
example_linear(3)    

O(nlogn): Quasilinear Time Complexity (擬線性時間，效率尚可)
執行時間會隨資料量呈nlogn增加，常見的有快速排序法或合併排序。之後文章會詳細介紹。

def mergeSort(mylist):
    if len(mylist) < 2:
        return mylist
    else:
        mid = len(mylist)//2
        leftlist = mylist[:mid]
        rightlist = mylist[mid:]
        return merge(mergeSort(leftlist), mergeSort(rightlist))

def merge(left, right):
    result = []
    while len(left) and len(right):
        if left[0] < right[0]:
            result.append(left.pop(0))
        else:
            result.append(right.pop(0))
    if len(left):
        result += left
    else:
        result += right
    return result

mylist = [10, 9, 20, 2, 16, 8]
print(mergeSort(mylist))

O(n^2): quadratic time complexity (平方時間，效率差)
執行時間會隨著資料量呈平方增加，通常兩層for迴圈(迴圈內有迴圈)就會造成這個效果。慢速排序法和選擇排序法都屬於此類。

def example_square(n):
    for i in range(n):
        for j in range(n):
            print(i,j)
example_square(3)

O(2^n): exponential time complexity (指數時間，效率差):

def fib(n):
    if n<=1:
        return n
    return fib(n-1)+fib(n-2)

O(n!): factorial time complexity (階層時間，效率差)
旅行推銷員問題。所有元素都在跑一次迴圈，將所有可能的排列組合都跑過一遍。

如果程式有多個宣告(multiple statements)，將全部的Big(O)相加，去掉係數與常數即可，之後每篇都可以看到BigO計算的範例。

本文主要為udemy課程: The Complete Data Structures and Algorithms Course in Python 的學習筆記，有興趣的人可以自己上去看看。
其他參考資料:
https://medium.com/traveling-light-taipei/%E6%BC%94%E7%AE%97%E6%B3%95%E7%AD%86%E8%A8%98-big-o-notation-3444f1932932
https://medium.com/appworks-school/%E5%88%9D%E5%AD%B8%E8%80%85%E5%AD%B8%E6%BC%94%E7%AE%97%E6%B3%95-%E5%BE%9E%E6%99%82%E9%96%93%E8%A4%87%E9%9B%9C%E5%BA%A6%E8%AA%8D%E8%AD%98%E5%B8%B8%E8%A6%8B%E6%BC%94%E7%AE%97%E6%B3%95-%E4%B8%80-b46fece65ba5
https://pjchender.dev/dsa/algo-intro/